一站式PHP后台解决方案
本文共 1658 字,大约阅读时间需要 5 分钟。
RXThinkCMF_TP6_PRO旗舰版 基于 ThinkPHP6 +Layui2.5.6 开发权限(RBAC)及内容管理框架,框架中集成了权限管理、模块管理、插件管理、钩子管理、数据库管理、富文本编辑器(已集成ueditor,kindeditor),后台支持多主题切换、布局管理、广告管理、配置管理、字典管理、切图管理、CMS内容管理等常用功能模块,以方便开发者快速构建自己的应用。RXThinkCMF_TP6_PRO框架专注于为中小企业提供最佳的行业基础后台框架解决方案,执行效率、扩展性、稳定性值得信赖,操作体验流畅,使用非常优化,欢迎大家使用及进行二次开发。
- 模块化:全新的架构和模块化的开发机制,便于灵活扩展和二次开发。
- 模型/栏目/分类信息体系:通过栏目和模型绑定,以及不同的模型类型,不同栏目可以实现差异化的功能,轻松实现诸如资讯、下载、讨论和图片等功能。通过分类信息和栏目绑定,可以自动建立索引表,轻松实现复杂的信息检索。
- RXThinkCMF_TP6_PRO是一套基于ThinkPHP + Layui开发出来的框架。
- 支持SQLServer、MySQL、Oracle、PostgreSQL、SQLite等多数据库类型。模块化设计,层次结构清晰。
- AUTH权限认证,操作权限控制精密细致,对所有管理链接都进行权限验证,可控制到导航菜单、功能按钮。提高开发效率及质量。
- 常用类封装,日志、缓存、验证、字典、文件(本地、七牛云)。等等,目前兼容浏览器(Chrome、Firefox、360浏览器等)
- 适用范围:可以开发OA、ERP、BPM、CRM、WMS、TMS、MIS、BI、电商平台后台、物流管理系统、快递管理系统、教务管理系统等各类管理软件。
环境要求:
PHP >= 7.0PDO PHP ExtensionMBstring PHP ExtensionCURL PHP Extension开启静态重写要求环境支持pathinfo要求安装Zip扩展(插件/模块市场需要)
功能特性
严谨规范: 提供一套有利于团队协作的结构设计、编码、数据等规范。高效灵活: 清晰的分层设计、钩子行为扩展机制,解耦设计更能灵活应对需求变更。严谨安全: 清晰的系统执行流程,严谨的异常检测和安全机制,详细的日志统计,为系统保驾护航。组件化: 完善的组件化设计,丰富的表单组件,让开发列表和表单更得心应手。无需前端开发,省时省力。简单上手快: 结构清晰、代码规范、在开发快速的同时还兼顾性能的极致追求。自身特色: 权限管理、组件丰富、第三方应用多、分层解耦化设计和先进的设计思想。高级进阶: 分布式、负载均衡、集群、Redis、分库分表。命令行: 命令行功能,一键管理应用扩展。
开发者信息
- 系统名称:RXThinkCMF_TP6_PRO权限(RBAC)及内容管理框架
- 作者[牧羊人]:南京RXThinkCMF研发中心
- 官网网址:
- 文档网址:
- 开源协议:Apache 2.0
后台演示(用户名:admin 密码:123456)
-
演示地址:
-
专业版仓库:
-
旗舰版仓库:
技术支持
技术支持QQ:tencent://message/?uin=1175401194
效果图展示
-
系统登录

-
系统主页
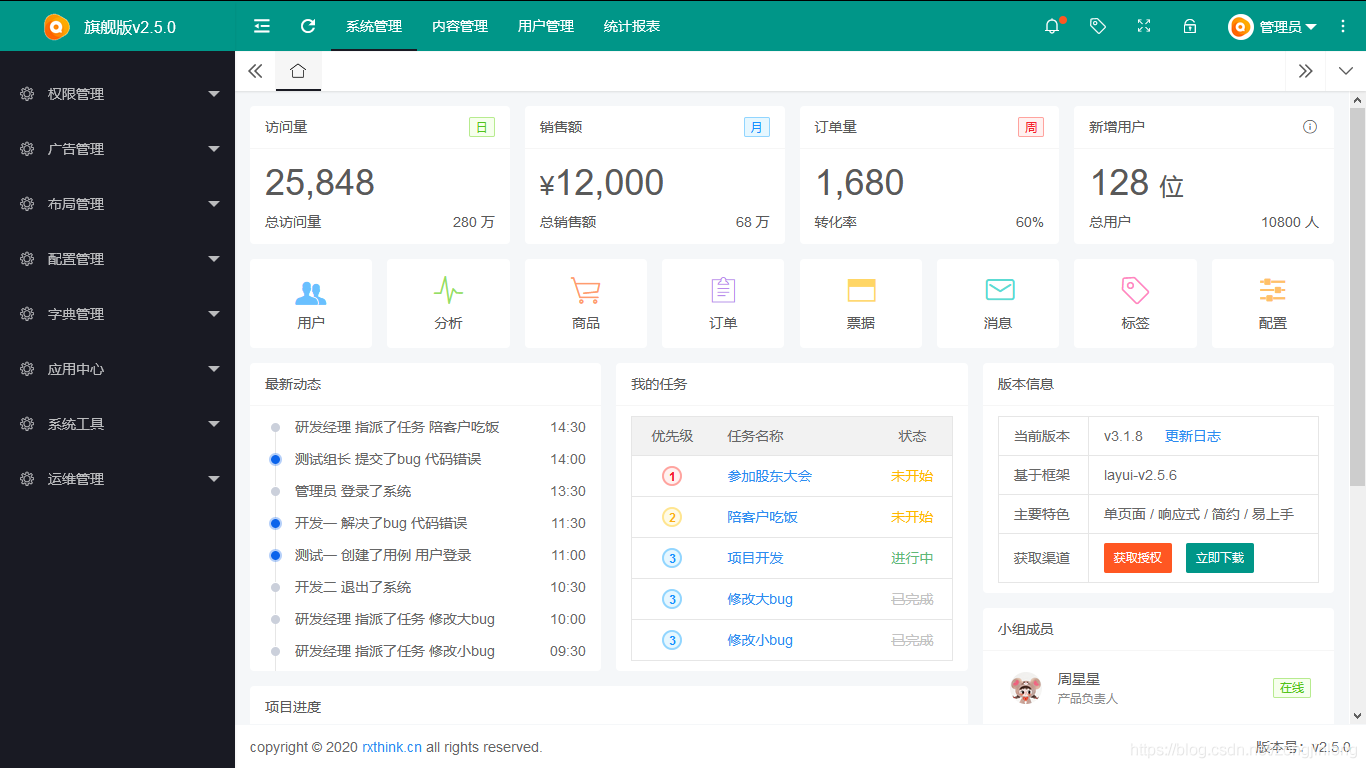
-
人员管理
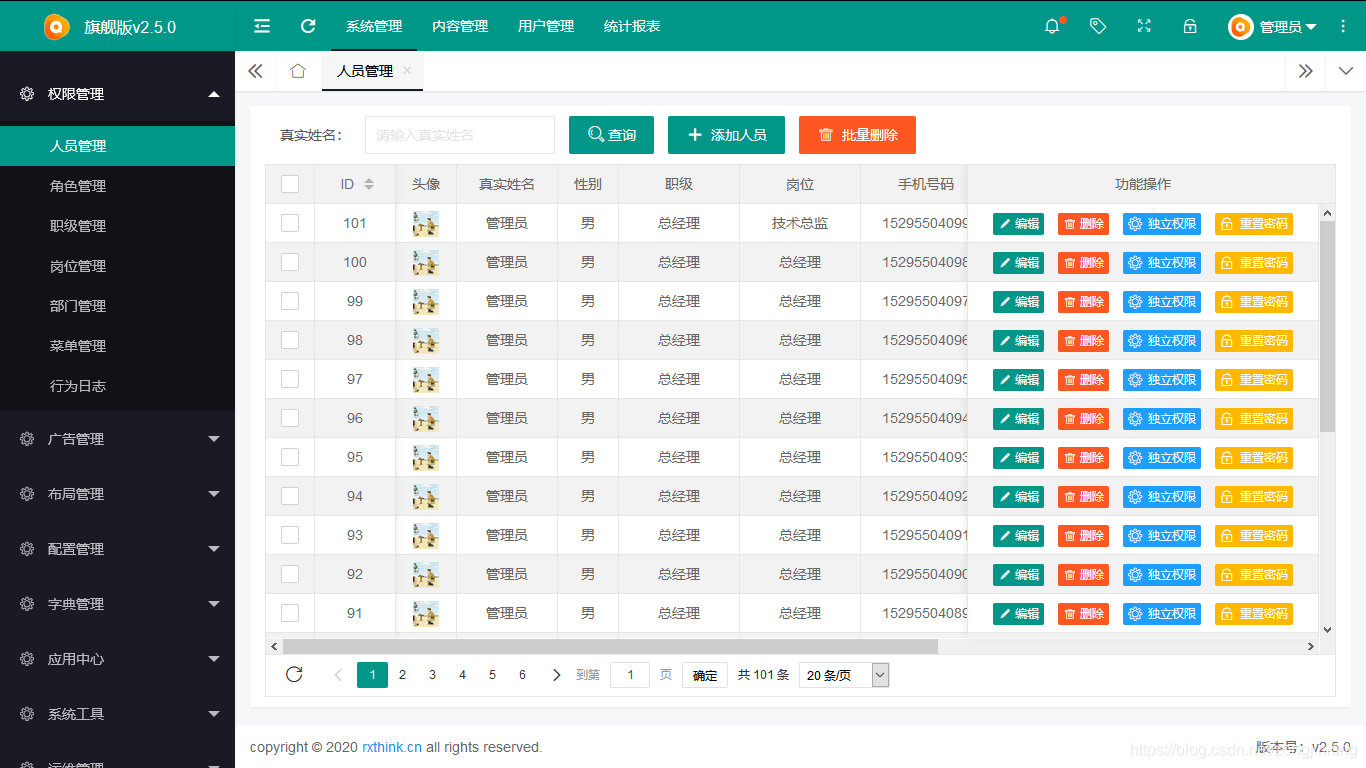
-
人员编辑
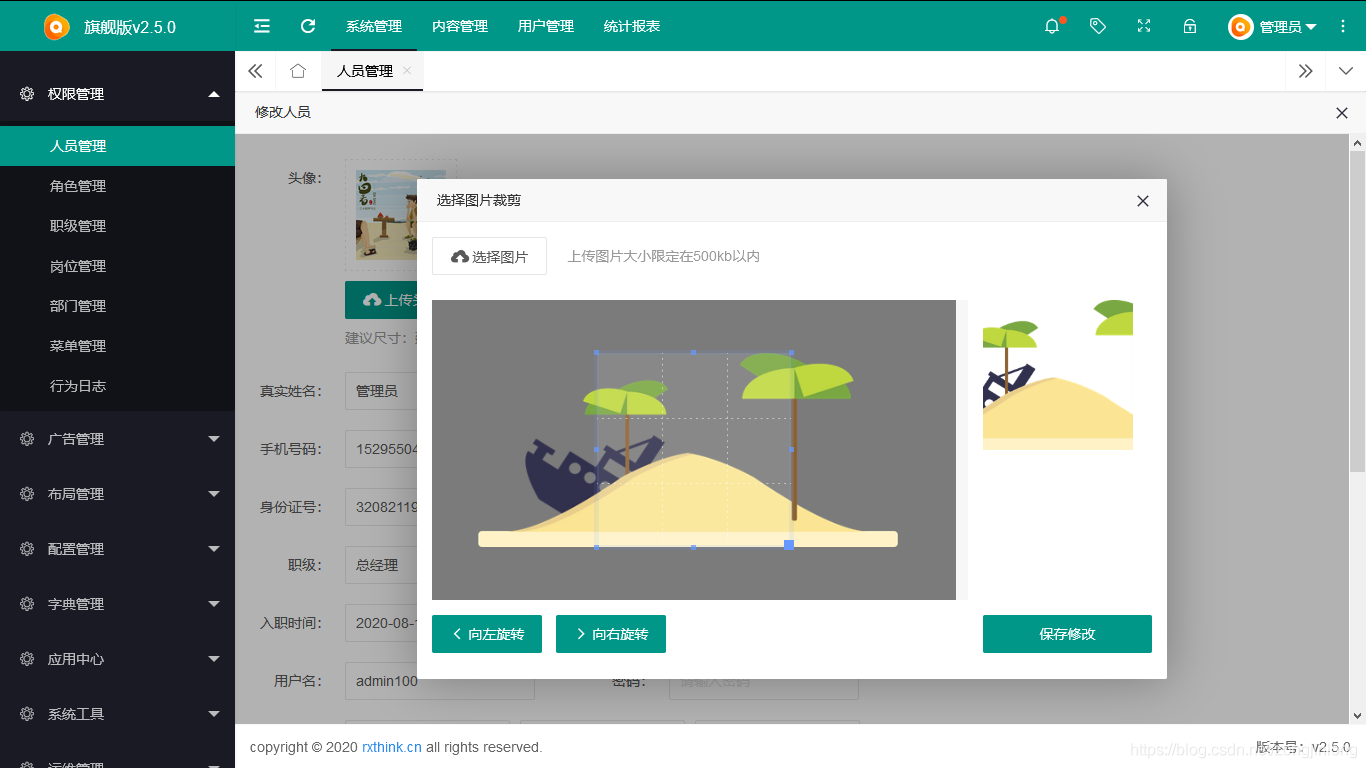
-
角色设置
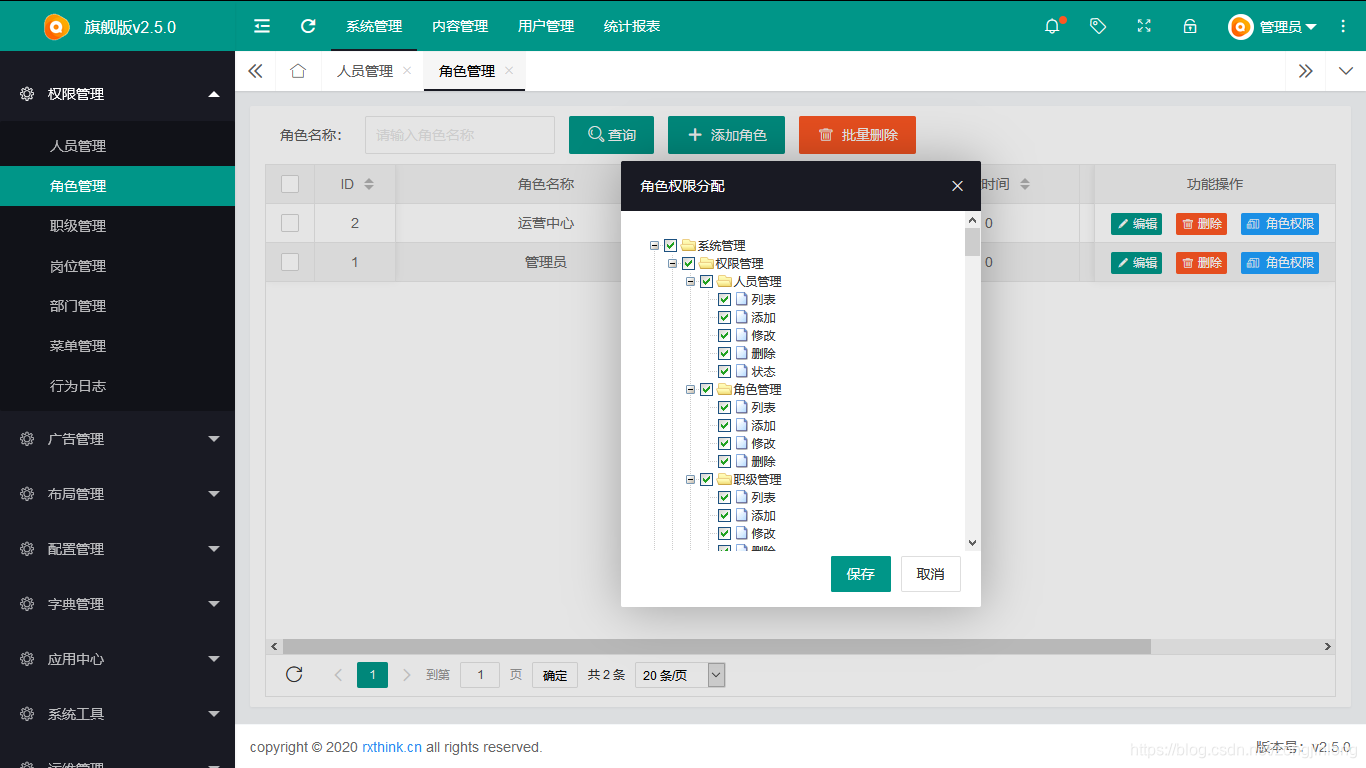
-
职级管理

-
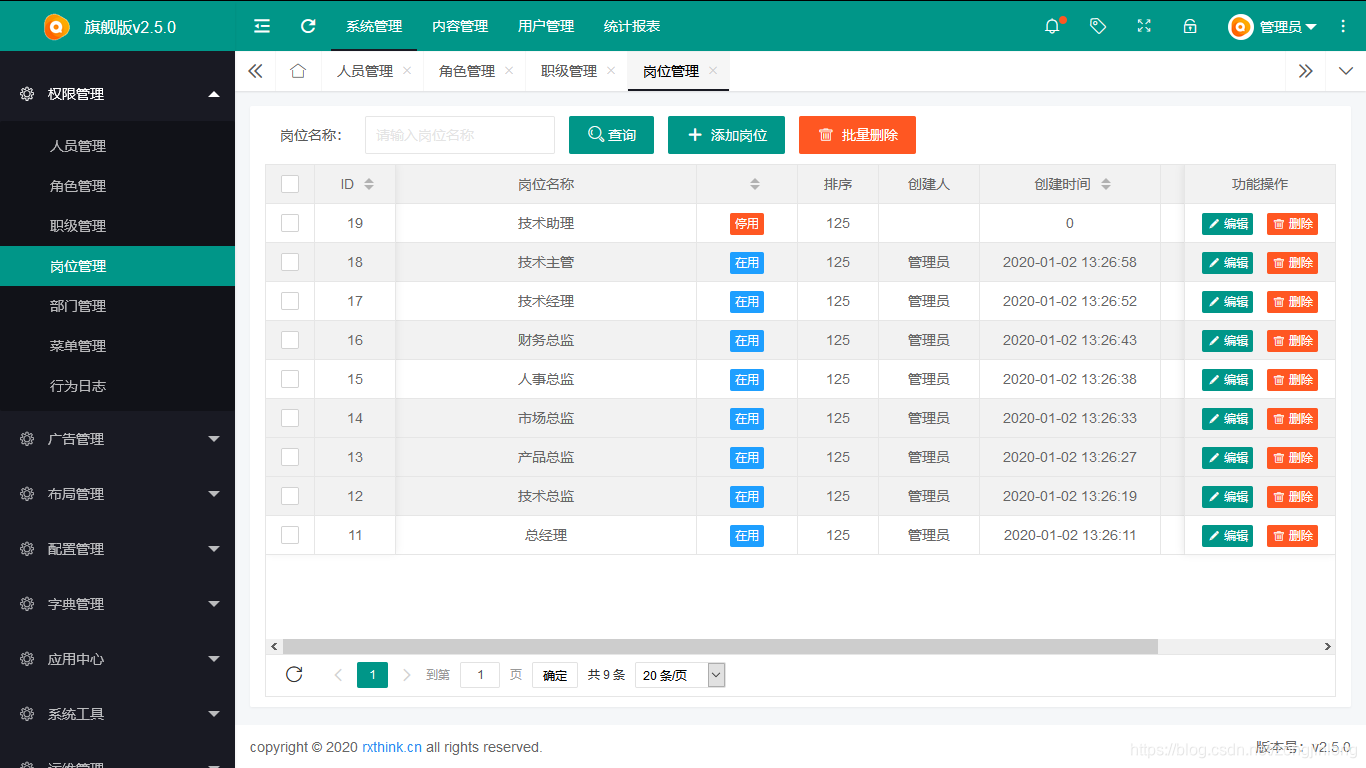
岗位管理
-
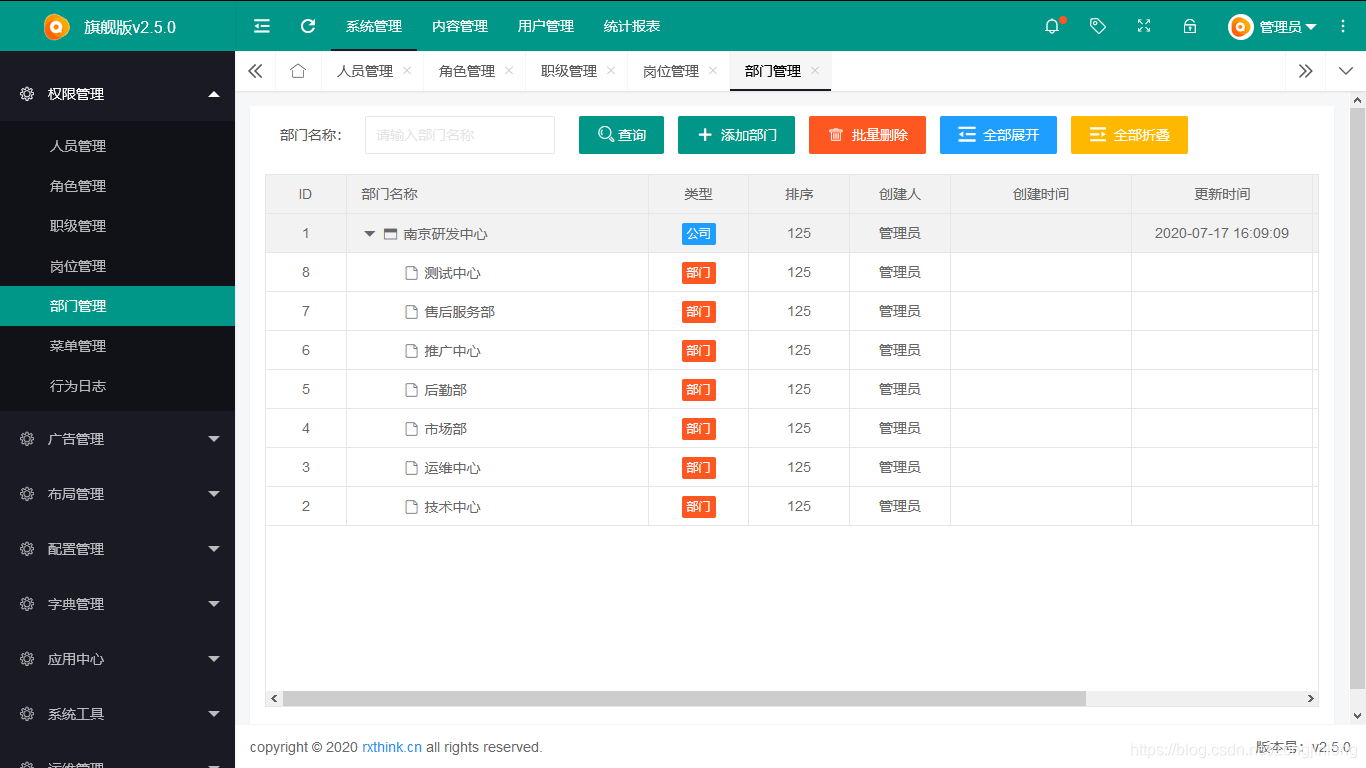
部门管理
-
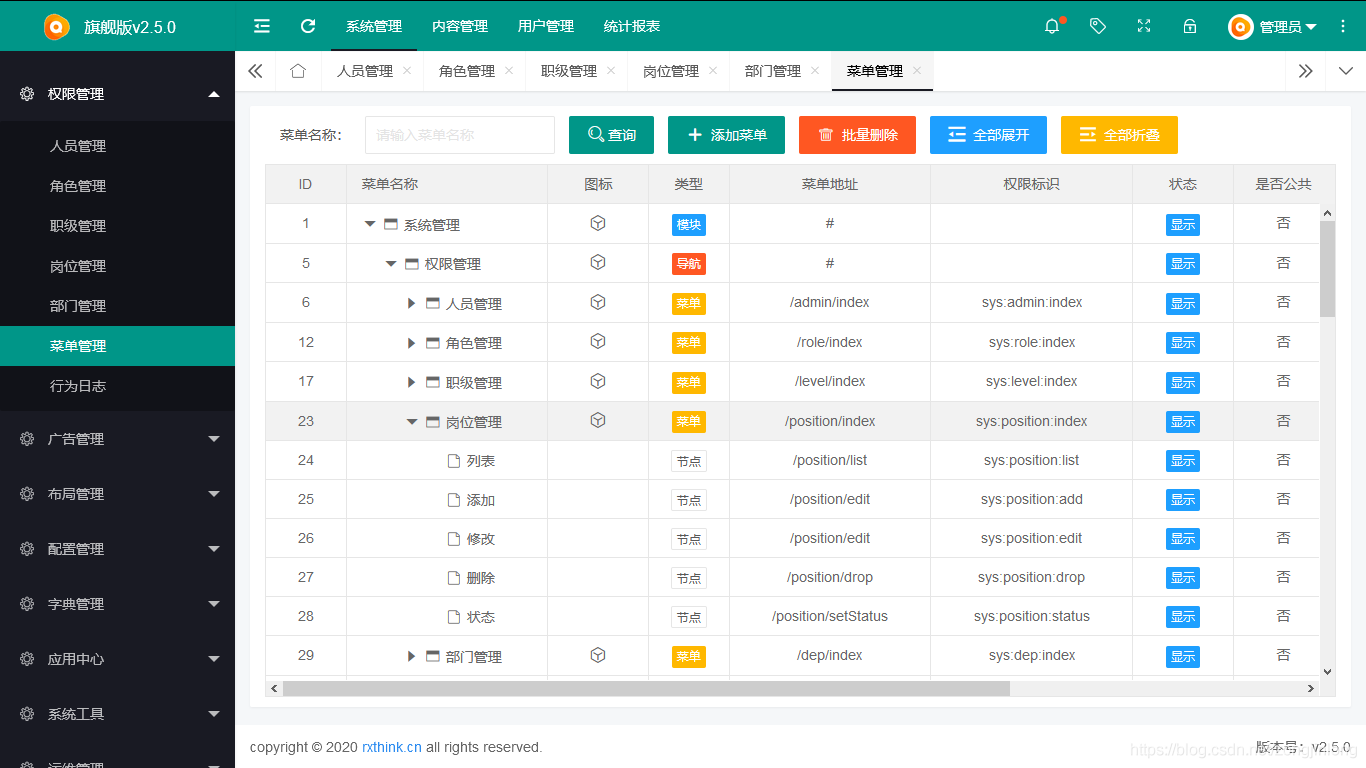
菜单管理
-
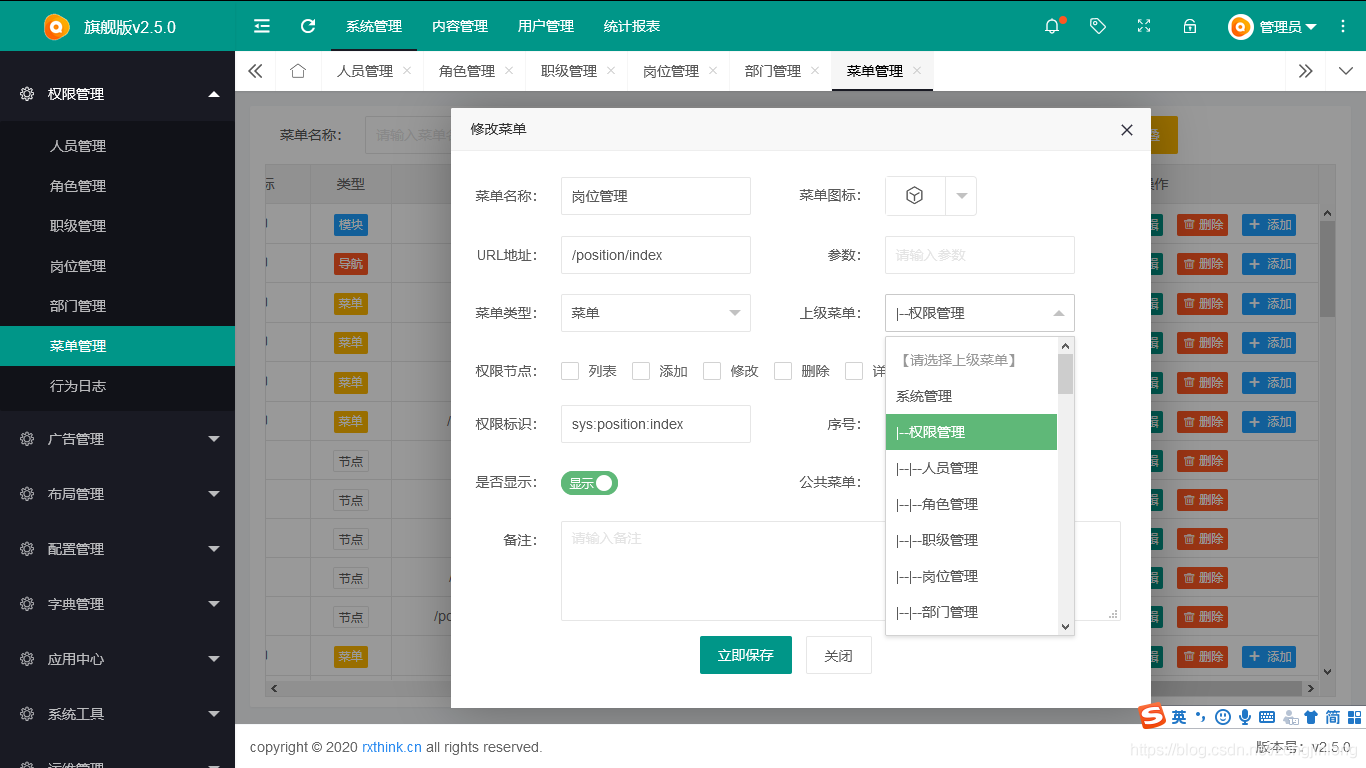
菜单编辑
-
广告管理
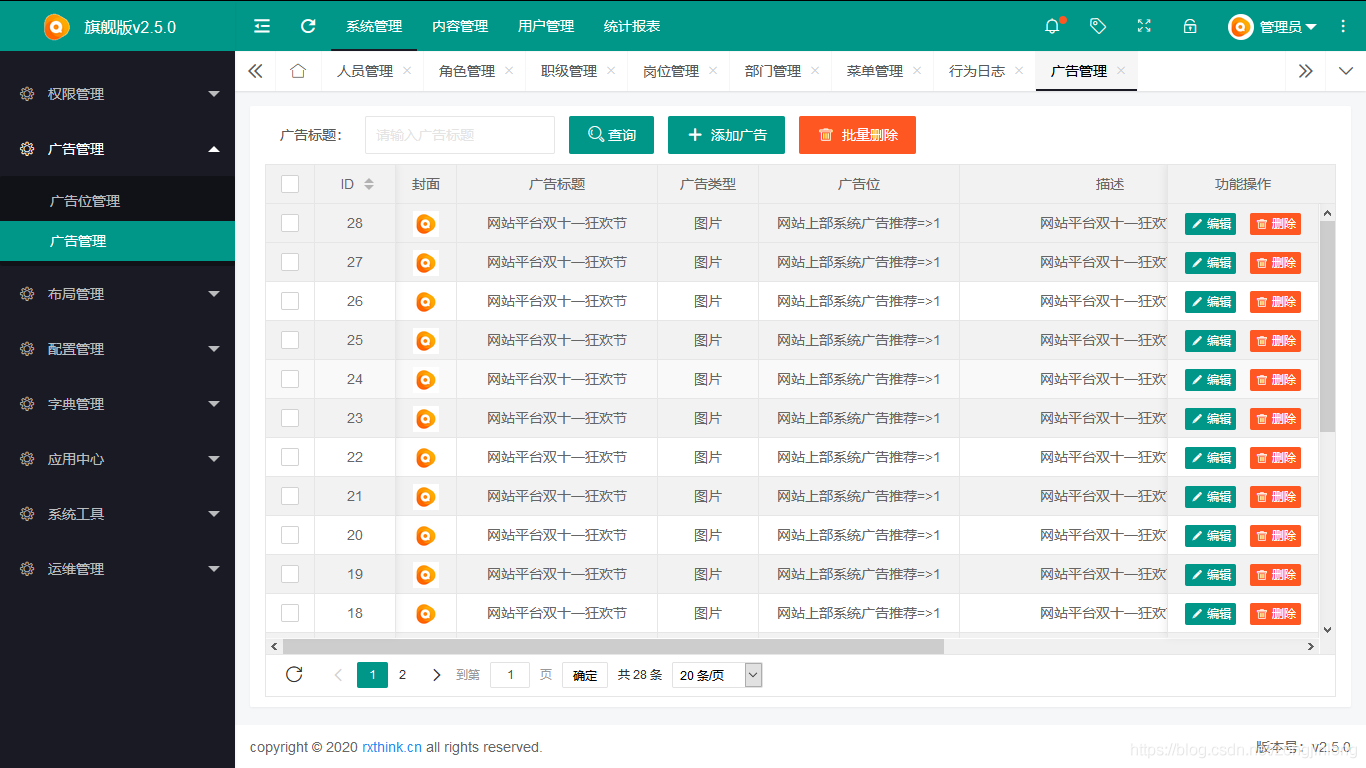
-
配置管理
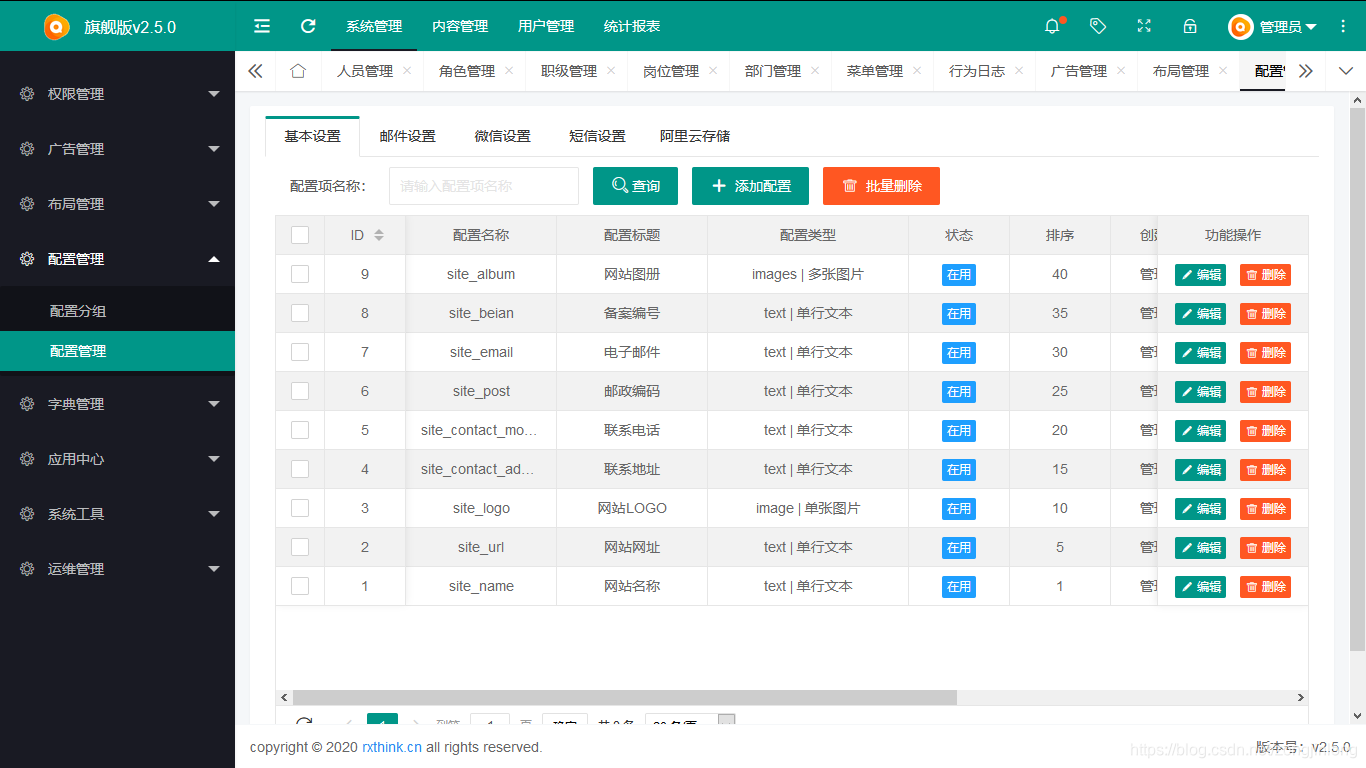
-
字典管理
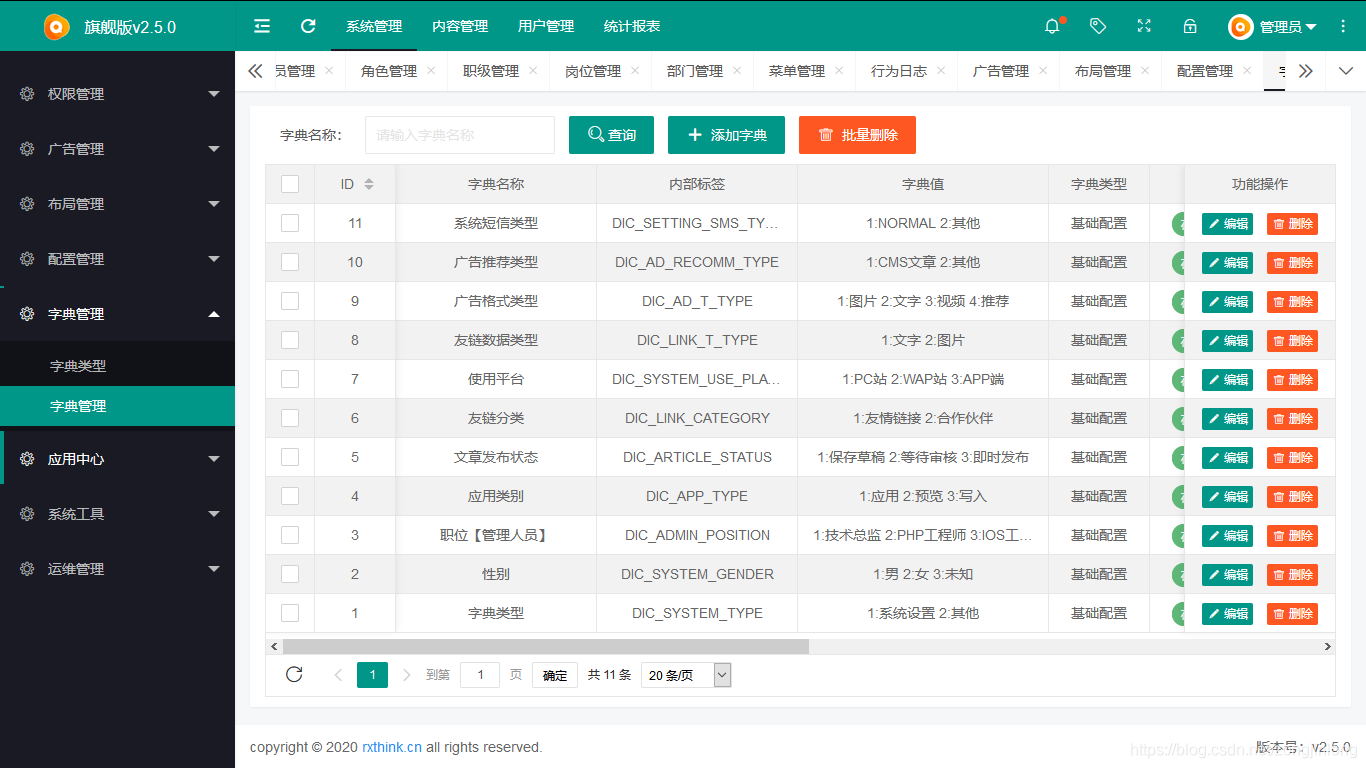
-
友情链接
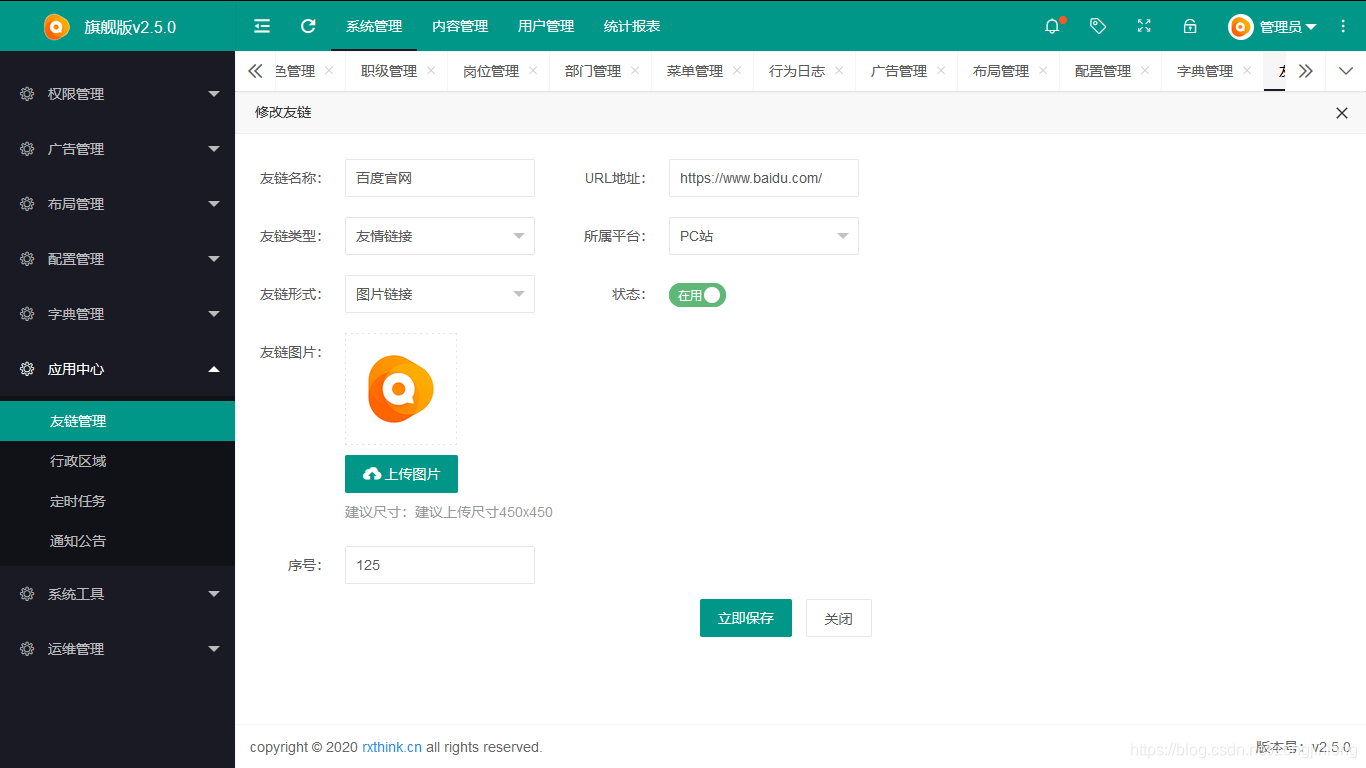
-
通知公告
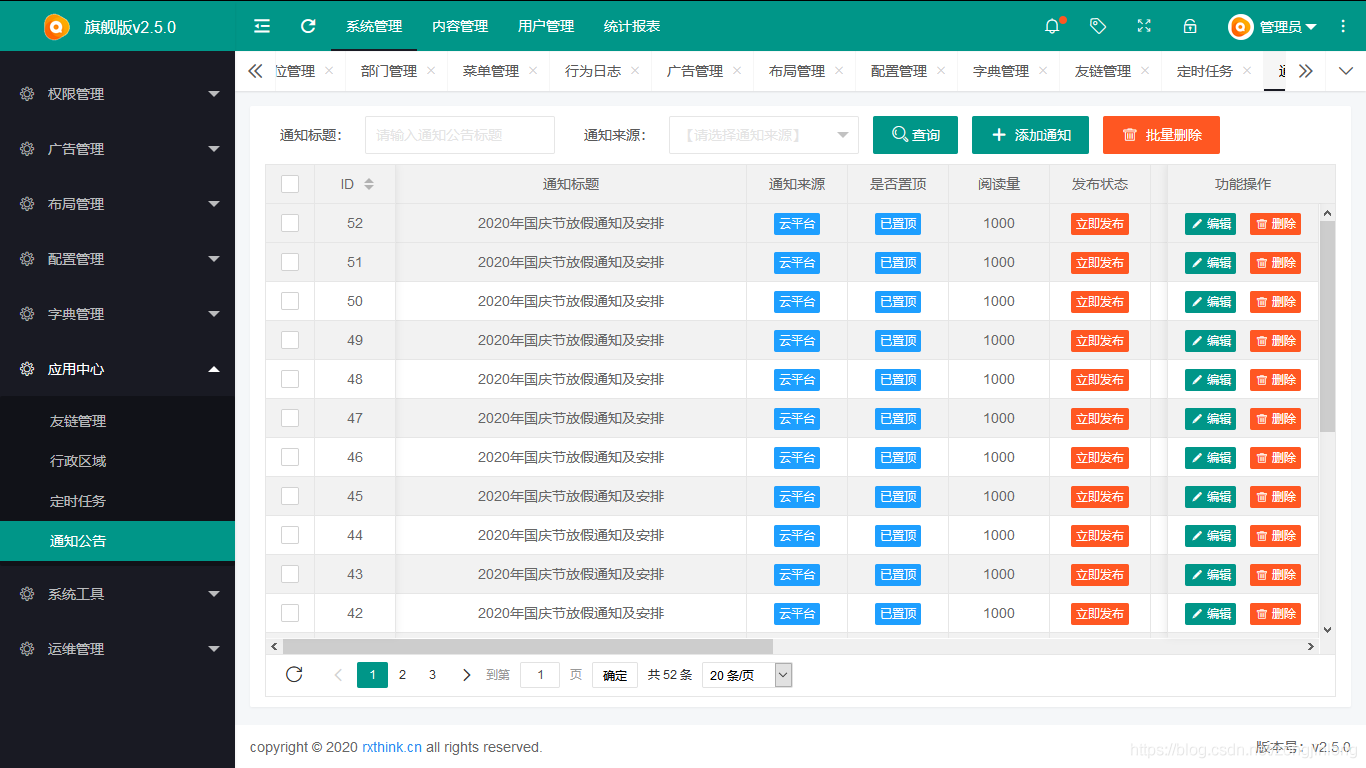
-
代码生成器
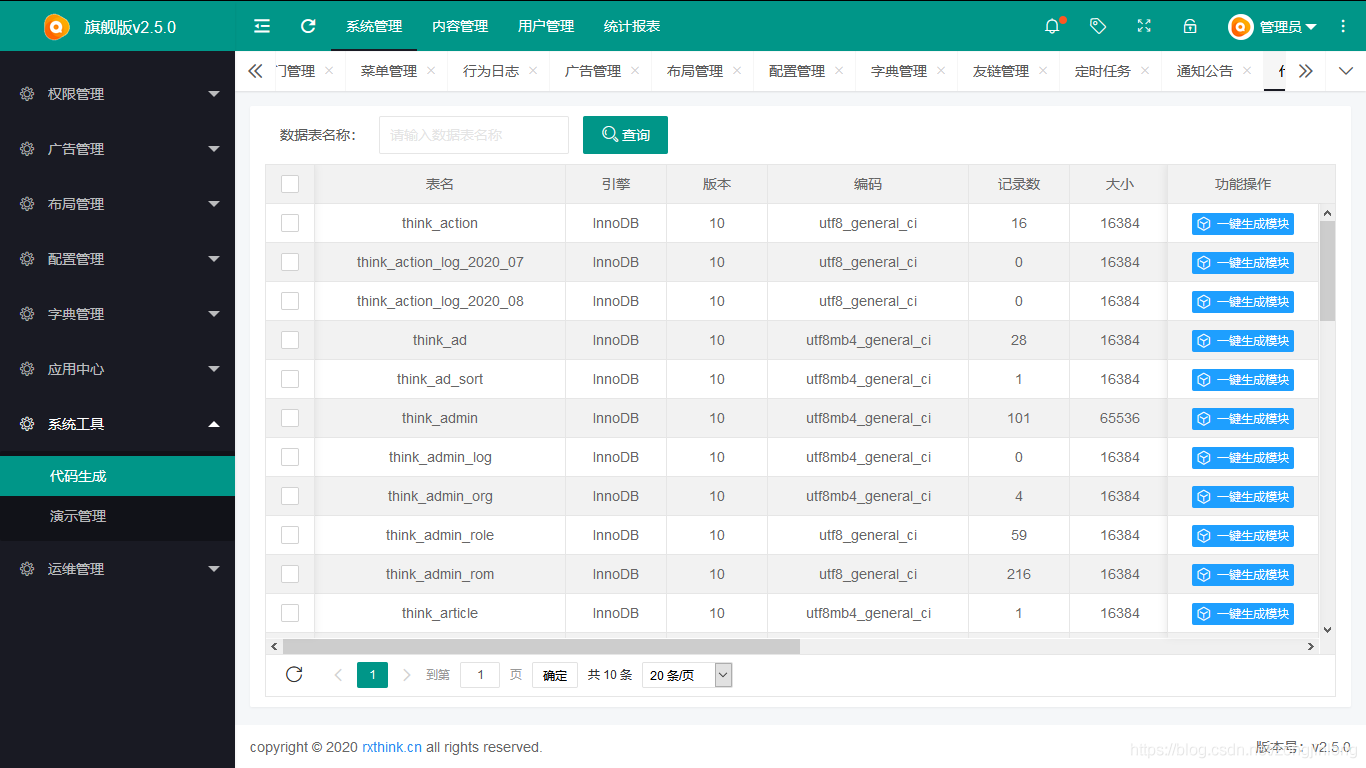
-
数据库管理
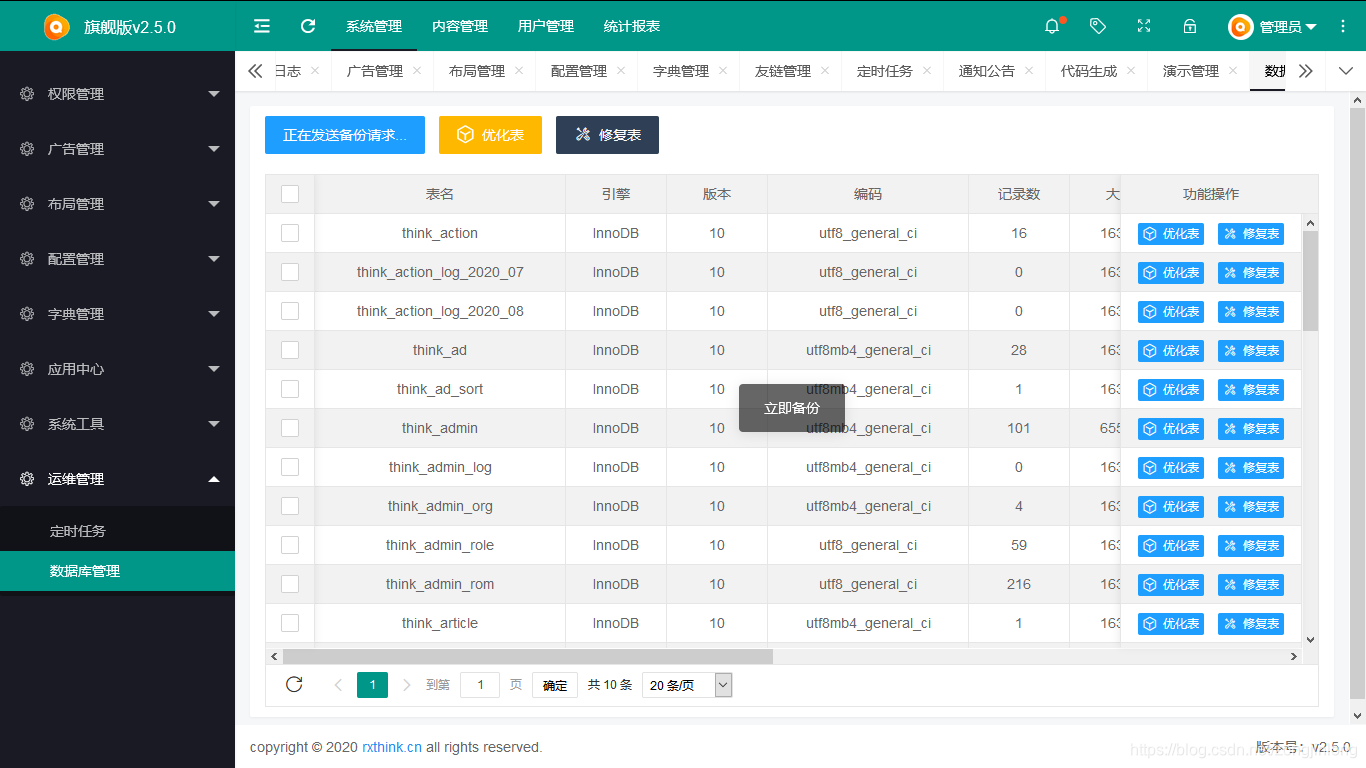
-
CMS管理
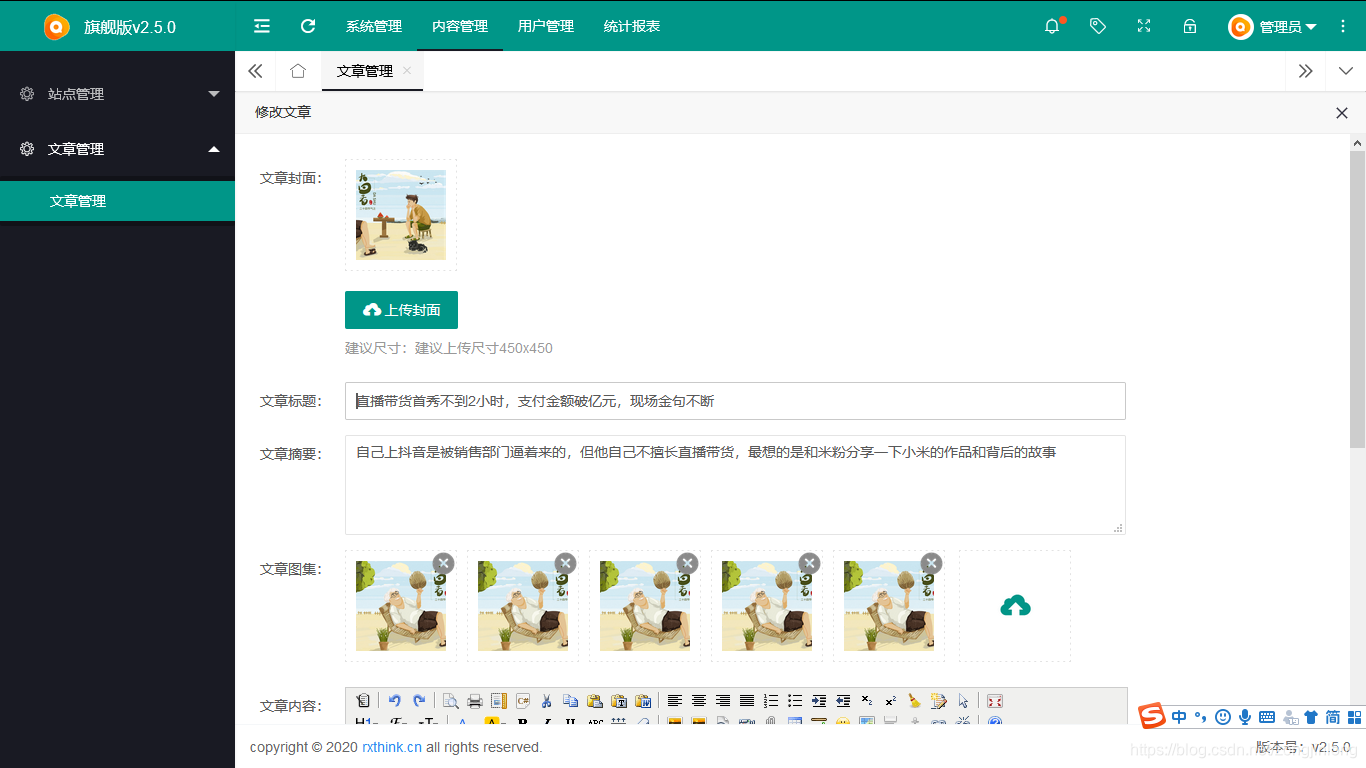
-
数据统计
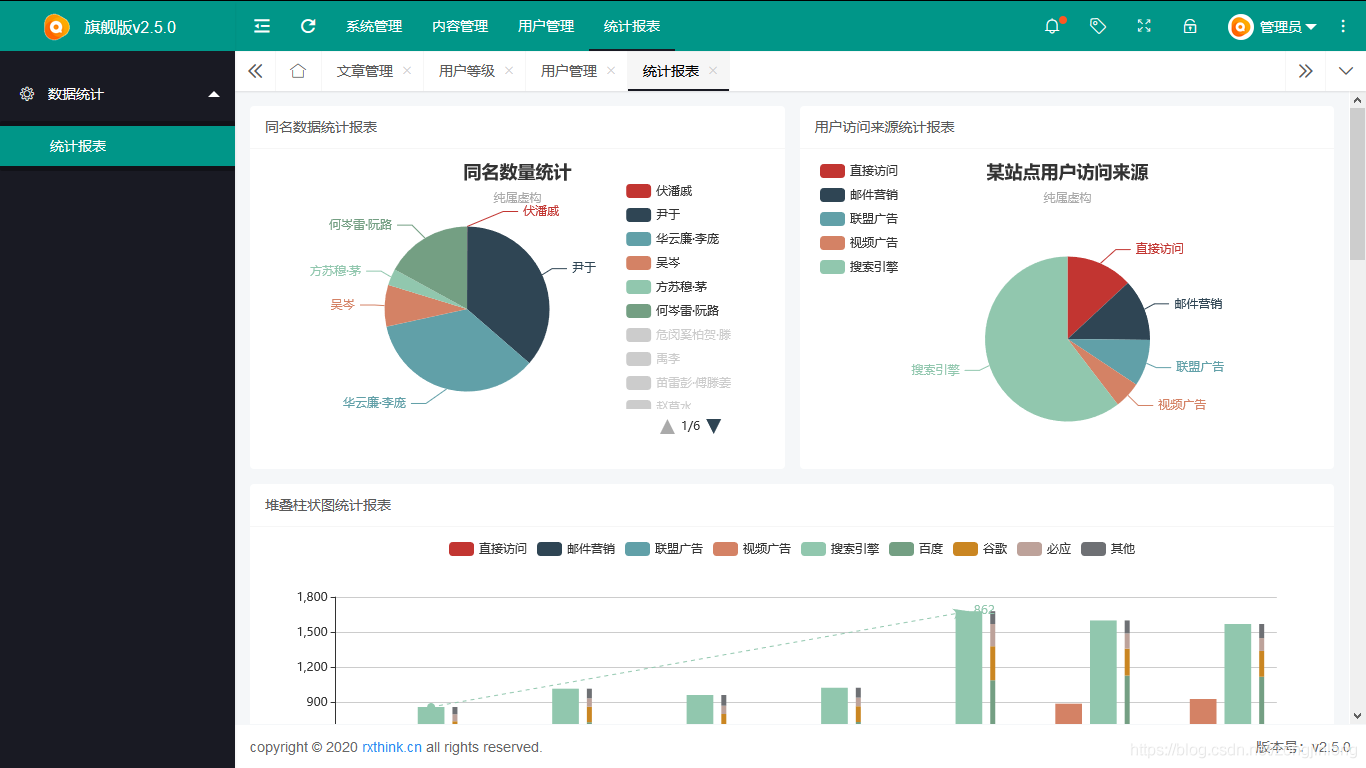
-
数据统计二

转载地址:http://ktenz.baihongyu.com/
你可能感兴趣的文章
Netty速成:基础+入门+中级+高级+源码架构+行业应用
查看>>
Netty遇到TCP发送缓冲区满了 写半包操作该如何处理
查看>>
Netty:ChannelPipeline和ChannelHandler为什么会鬼混在一起?
查看>>
Netty:原理架构解析
查看>>
Network Dissection:Quantifying Interpretability of Deep Visual Representations(深层视觉表征的量化解释)
查看>>
Network Sniffer and Connection Analyzer
查看>>
Network 灰鸽宝典【目录】
查看>>
Networkx写入Shape文件
查看>>
NetworkX系列教程(11)-graph和其他数据格式转换
查看>>
Networkx读取军械调查-ITN综合传输网络?/读取GML文件
查看>>
network小学习
查看>>
Netwox网络工具使用详解
查看>>
Net与Flex入门
查看>>
net包之IPConn
查看>>
Net操作配置文件(Web.config|App.config)通用类
查看>>
NeurIPS(神经信息处理系统大会)-ChatGPT4o作答
查看>>
neuroph轻量级神经网络框架
查看>>
Neutron系列 : Neutron OVS OpenFlow 流表 和 L2 Population(7)
查看>>
NEW DATE()之参数传递
查看>>
New Relic——手机应用app开发达人的福利立即就到啦!
查看>>